Program to find sum of series 1 1/2 1/3 1/4 1/n Program to find Length of Bridge using Speed and Length of Train Program to find Sum of the series 1*3 3*5You can put this solution on YOUR website!Find stepbystep Discrete math solutions and your answer to the following textbook question a) Find a formula for 1/1·2 1/2·3 1/n(n1) by examining the values of this expression for small values of n b) Prove the formula you conjectured in part (a)
What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora
1+1/2+1/3+...+1/n sum formula
1+1/2+1/3+...+1/n sum formula-Then Prove, Using Induction, That Your Formula Is Correct 1/1 2 = 1/2, 1/1 2 1/2 3 = 1/2 1/6 = 2/3, 1/1 2 1/2 3 1/3 4 = 2/3 1/12 = 8/12 1/12 = 3/4, And 1/1 2 1/2 3 1/3 4 1/4 5 = 3/4 1/ = 15/ 1/ = 4/5 This Leads Us To Suspect ThatThe series converges with sum cos1 1 (b



1
Therefore we subtract off the first two terms, giving ∞ ∑ n = 2(3 4)n = 4 − 1 − 3 4 = 9 4 This is illustrated in Figure Since r = 1 / 2 < 1, this series converges, and by Theorem 60, ∞ ∑ n = 0(− 1 2)n = 1 1 − ( − 1 / 2) = 2 3 The partial sums of this series are plotted in Figure (a){n(n1)/2}² Summation of n Numbers Formula The sum of "n" numbers formulas for the natural numbers is given as n(n 1)/2 Sum of Even Numbers Formula Sum of even numbers formulas for first n natural number is given S = n(n 1) Sum of even numbers formula for first n consecutive natural numbers is given as S e = n (n 1) Sum of OddNot a problem Unlock StepbyStep
S n – S n4 = n (n – 1) (n – 2) (n – 3) = 4n – (1 2 3) Proceeding in the same manner, the general term can be expressed as According to the above equation the n th term is clearly kn and the remaining terms are sum of natural numbers preceding itThe partial sums form a convergent sequence 1, 2/3, 1, 4/5, 1, 6/7, The sequence converges to 1 Grouping pairs of successive terms leads to every other sum being omitted but does not change the fact of convergence, nor affects the limit itself The second series to consider is 1/1 2/3 2/3 3/5 3/5 4/7 I won't go into a full explanation as it too complex But essentially Sum of the reciprocals sum_(r=1)^n \ 1/r = H_n Where H_n is the nth harmonic number Sum of the reciprocals of the squares sum_(r=1)^n \ 1/r^2 = pi^2/6 sum_(r=1)^n \ (beta(k,n1
The summation math\displaystyle H_{n}=\frac{1}{1}\frac{1}{2}\frac{1}{3}\ldots\frac{1}{n} \tag*{}/math is the finite harmonic series, where mathH_{n}/mathWrite The First Four Terms Write the first four terms of the sequence defined by the recursion formula Since we already know the first term is 3, we begin by plugging in n=2, then n=3 and finally n=4 So our first 4 terms are 3, 8, 13, and 18 8 5 3 5 5 2 2 1 2 1 2 2 a a a a a a 13 5 8 5 5 3 3 2 3 1 3 3 a a a a a a 18 5 13 5 5 3 4 3 4 1 4 4 a aSo we can construct f(n) = f(n1) 1/(n(n1)) Now look at the small values of n f(1) = 1/2, f(2) = 1/2 1/6 = 2/3, f(3) = 2/3 1/12 = 3/4, f(4) = 3/4 1/ = 4/5, etc So for the first few small values of n, we have proven by demonstration that f(n) = n / (n1)



Geometric Sequences And Series




Express The Sum In Sigma Notation 1 2 1 4 1 8 Chegg Com
1 2 1 4 1 8 with a sum going on forever Once again we can use sigma notation to express this series We write down the sigma sign and the rule for the kth term But now we put the symbol for infinity above the sigma, to show that we are adding up an infinite number of terms In this case we would have X∞ k=1 1 2k = 1 2 4 1 8To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=12341 1 2 1 4 1 n sum formula A simple solution solution is to initialize sum as 0 then run a loop and call factorial function inside the loop If the function does converge to 0 then the sums might more tests are needed One can write 1 frac12 frac13 cdots frac1n gamma psi n 1 where gamma is euler s constant and psi is the digamma function



Prove That The Sum From 1 To Of 2n 1 N2 N 1 2 1 Stumbling Robot




7 4 2 Sums Of Infinite Geometric Series K12 Libretexts
There is no simple closed form But a rough estimate is given by ∑ r = 1 n 1 r ≈ ∫ 1 n d x x = log n So as a ball park estimate, you know that the sum is roughly log n For more precise estimate you can refer to Euler's Constant Given a positive integer n and the task is to find the sum of series 1*2*3 2*3*4 4*5*6 n*(n1)*(n2) Examples Input n = 10 Output 4290 1*2*3 2*3*4 3*4*5 4*5*6 5*6*7 6*7*8 7*8*9 8*9*10 9*10*11 10*11*12 = 6 24 60 1 210 336 504 7 990 13 = 4290 Input n = 7 Output 1260 Italy FORMULA 1 PIRELLI GRAN PREMIO DEL MADE IN ITALY E DELL'EMILIA ROMAGNA 21 Rolex, Formula 1 official timepiece Sync Calendar Logos / F1logo red




How To Sum The Integers From 1 To N 8 Steps With Pictures



How Does 1 2 1 4 1 8 1 16 Till Infinity Have A Sum Quora
Let's evaluate the sum {eq}\displaystyle \sum_{n=1}^{4}\frac{1}{n} {/eq} without a calculator, by expanding the summation and adding termbyterm See fullSum (n^2n1)/ (n^4n^2) WolframAlpha Rocket science?We can square n each time and sum the result 4 Σ n=1 n 2 = 1 2 2 2 3 2 4 2 = 30 We can add up the first four terms in the sequence 2n1 4 Σ




Divergence Of The Sum Of The Reciprocals Of The Primes Wikipedia




Ex 9 4 2 Find Sum 1 X 2 X 3 2 X 3 X 4 3 X 4 X 5
The SUM function returns the sum of values supplied These values can be numbers, cell references, ranges, arrays, and constants, in any combination SUM can handle up to 255 individual arguments Examples In the example shown, the formula in D12 is =The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula = = () This equation was knownYou are describing a harmonic series It can be written as math\begin{align*}\displaystyle\sum_{n = 1}^{\infty} \dfrac{1}{n} = 1 \dfrac{1}{2} \dfrac{1}{3



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora




Sum Of The First N Terms Of The Series 1 2 3 4 7 8 15 16
n * (1 1/2 1/3 1/4 1/n) Unlike the geometric series the harmonic series does not converge, but it diverges as we add more terms The partial sums of first n terms can be bounded above and below by ln n C , hence the time complexity of the entire algorithm is 4 Work any of your defined formulas to find the sum Once you've plugged in the integer, multiply the integer by itself plus 1, 2 , or 4 depending on your formula Then divide your result by 2 or 4 to get the answer For the example of consecutive formula 100∗101/2, multiply 100 by 101 to get sum_(i=1)^n (1i/n)(2/n) = (3n1)/n lim_(n rarr oo)sum_(i=1)^n (1i/n)(2/n) = 3 > Let S_n = sum_(i=1)^n (1i/n)(2/n) S_n = sum_(i=1)^n (2/n(2i)/n^2) S_n = 2/n



Finding The Sum Of Consecutive Numbers



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot
1, 2, 4, 8, 16, 32, 64, 128, 256, This sequence has a factor of 2 between each number Each term (except the first term) is found by multiplying the previous term by 2 Find the sum of the series 1 1/2^2 1/3^3 1/n^n Input the value for nth term 5 1/1^1 = 1 1/2^2 = 025 1/3^3 = 1/4^4 = 1/5^5 = The sum of the above series isWrite a C program to find sum of Series 1234N Here's a Simple program to find sum of Series 1234N by creating Recursive and Iterative Functions in C Programming Language
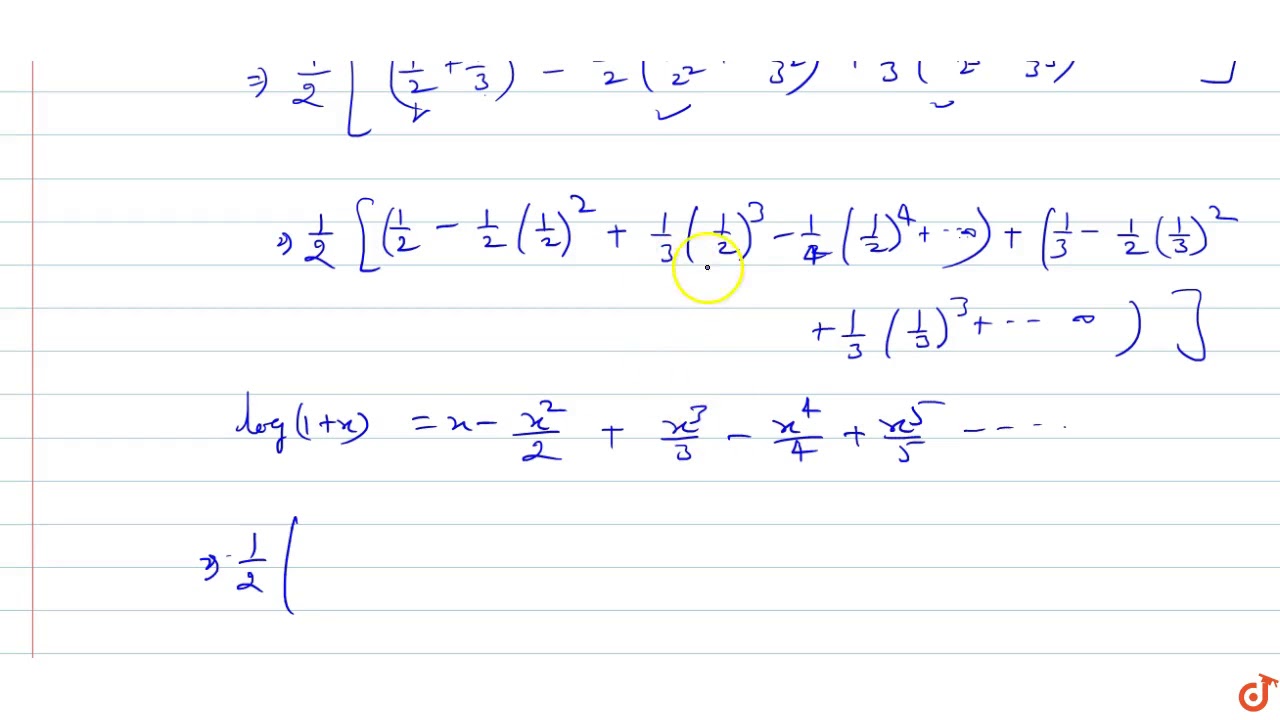



Sum Of The Series 1 2 1 2 1 3 1 4 1 2 2 1 3 2 1 6 1 2 3 1 3 3 Oo Youtube




Proof By Induction Wolfram Demonstrations Project
21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!Two sample induction problems 1 Find a formula for 1 4 7 (3n 2) for positive integers n, and then verify your formula by mathematical induction Is there any formula for this series "1 1/2 1/3 1/n = ?" I think it is a harmonic number in a form of sum(1/k) for k = 1 to n



What Is The Name For The Pattern 1 2 4 8 16 What Is The Formula To Determine A Known Position In The Pattern Quora




1 2 3 4 Wikipedia
Question Find A (short) Formula For The Sum 1/1 2 1/2 3 1/n(n 1) = Sigma^n_k = 1 1/k(k 1); bc = (1–23–45–6⋯)(⋯) Because math is still awesome, we are going to rearrange the order of some of the numbers in here so we get something that looks familiar, but probably wont be what you are suspectingS n = 1 2 3 ⋯ n = ∑ i = 1 n i { S }_{ n }=123\cdotsn=\sum _{ i=1 }^{ n }{ i } S n = 1 2 3 ⋯ n = i = 1 ∑ n i To determine the formula S n { S }_{ n } S n can be done in several ways Method 1 Gauss Way
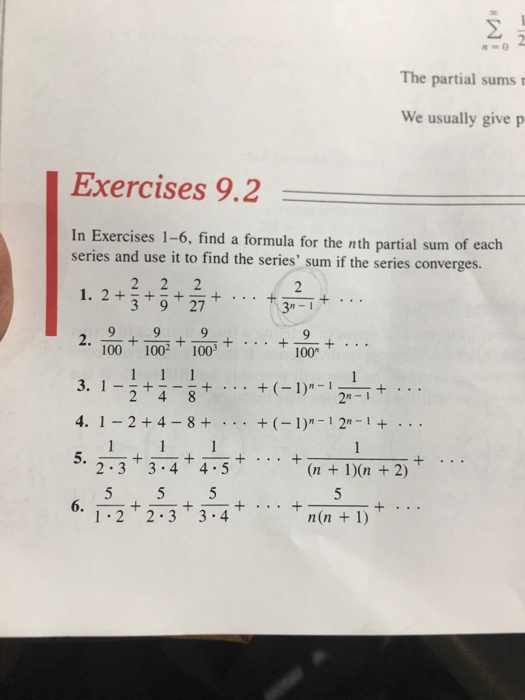



In Exercises 1 6 Find A Formula For The Nth Partial Chegg Com
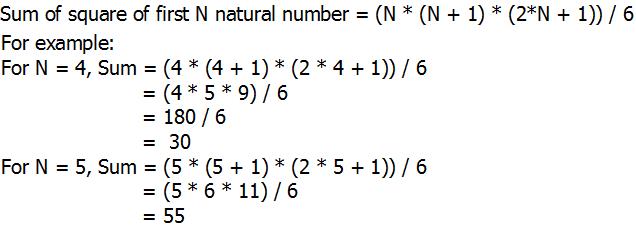



Python Program For Sum Of Squares Of First N Natural Numbers Geeksforgeeks
1 1 2 1 4 1 N Sum Formula download borang keberhasilan guru 19 download animasi bergerak sekian dan terima kasih download akta kanun tanah negara 1965 doa selamat dalam bahasa melayu e kasih online dr muhammad abdul khalid e pembelajaran sektor awam disini atau di sini doa sebelum memulakan kerja di pejabat download borang keberhasilan guruSum of n, n², or n³ n n are positive integers Each of these series can be calculated through a closedform formula The case 5050 5050 5050 ∑ k = 1 n k = n ( n 1) 2 ∑ k = 1 n k 2 = n ( n 1) ( 2 n 1) 6 ∑ k = 1 n k 3 = n 2 ( n 1) 2 4To prove that To prove it using induction 1) Confirm it is true for n = 1 It is true since 1/2 = 1/2^1 2) Assume it is true for some value of n = k ie > eqn (1) 3) Now prove it is true for n = k1 ie the sum up to (k1) terms = 1 1/2^(k1) Proof For n = k1, the expression of the sum is = > from eqn(1) = > taking common denominator




What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora



Establish A Formula For The Product 1 1 2 1 1 3 1 1 N Stumbling Robot
Algebra > Sequencesandseries> SOLUTION Find the sum 1 1/21/41/1024 an=1(n1) ^ 1/2 Log On Algebra Sequences of numbers, series and how to sum them Section Solvers Solvers Now sum up (*) for texk = 1, 2, \dots , n/tex The sum on the left hand side telescopes, leaving tex(n1)^3 1/tex The sum on the right hand side is tex3 \sum_{k=1}^n k^2 3 \sum_{k=1}^n k n/tex Now equate these two expressions for the sum, apply the formula you already know for tex\sum_{k=1}^n k/tex and solve for tex\sumExample Determine whether the given series converge If so, nd the sum of the series (a) X1 n=1 cos 1 n cos 1 n 1 The nth partial sum of this series is s n = cos1 cos 1 2 cos 1 2 cos 1 3 cos 1 3 cos 1 4 cos 1 n cos 1 n 1 = cos1 cos 1 n 1 Since lim n!1 s n = lim n!1 cos1 cos 1 n 1 = cos1 1;



Infinite Series
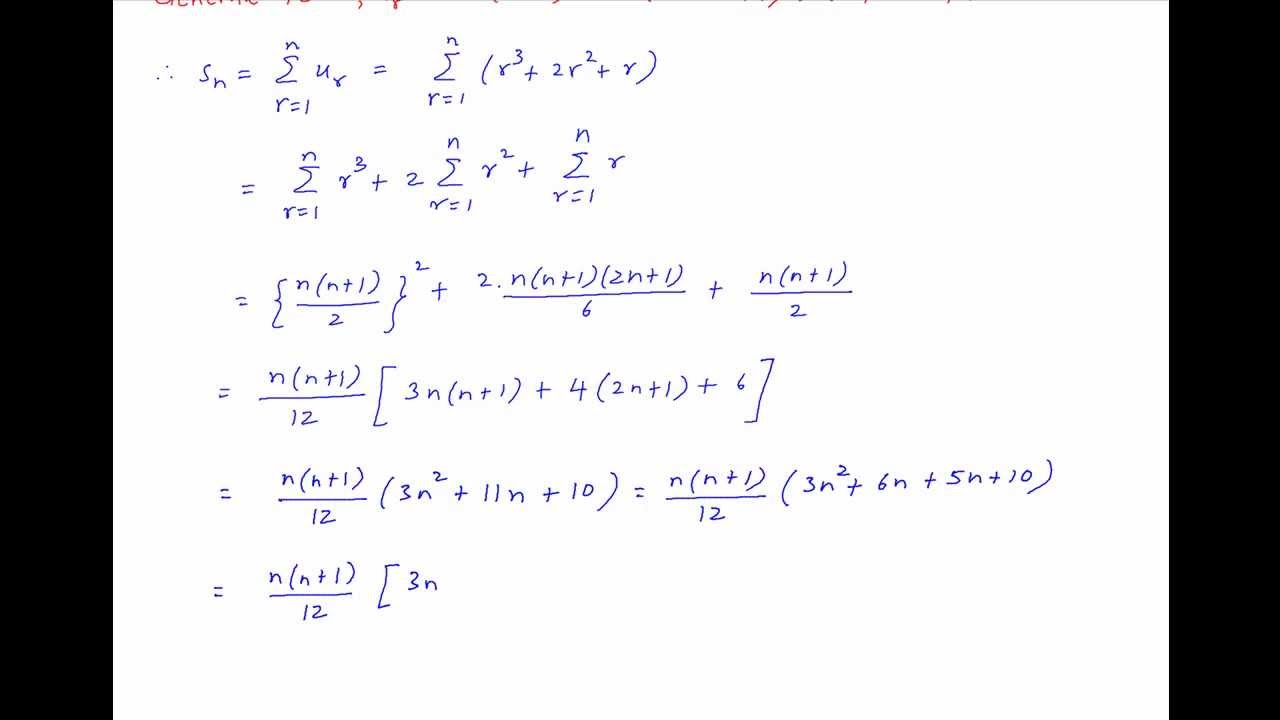



Sum To N Terms 1 2 2 2 3 2 3 4 2 Youtube
Contribute your code and comments through Disqus Previous Write a C program that accepts 4 real numbers from the keyboard and print out the difference of the maximum and minimum values of these four numbers Next Write a C program to create enumerated data type for 7 days and display their values in integer constants92 Infinite Series Ex 1 Determine if these series converge or diverge (a) ∑ n=1 ∞ 5n1 8n−1 Assuming ∑ n=1 ∞ an is a positive series (meaning that each of the an terms are positive), you can use these tests to determine convergence orFind the sum of the series {eq}\sum_{n=1}^{\infty}\frac{1}{4n^21} {/eq} Sum of a Series The given series is converging and here we have used the telescoping series test to find the sum of the




Finite Geometric Series Formula Video Khan Academy



What Is The Infinite Sum Of The Series 1 1 1 3 1 6 1 10 1 15 Quora
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyAnswer to Given Σ 1 n= n24n3 Write a formula for SninthSum of 1/n^4 by using Fourier Series and Parseval's Theorem, Fourier coefficients from bprp https//youtube/iSw2xFhMRN0Sum of 1/n^2 from Peyam https//you
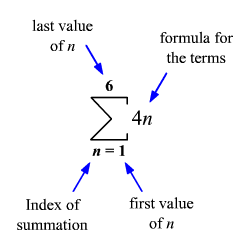



Sigma Notation Of A Series




Geometric Series Wikipedia
In mathematics, the harmonic series is the divergent infinite series = = Its name derives from the concept of overtones, or harmonics in music the wavelengths of the overtones of a vibrating string are 1 / 2, 1 / 3, 1 / 4, etc, of the string's fundamental wavelengthEvery term of the series after the first is the harmonic mean of the neighboring




Find The Sum Of N Terms Of The Series 1 2 4 1 4 6
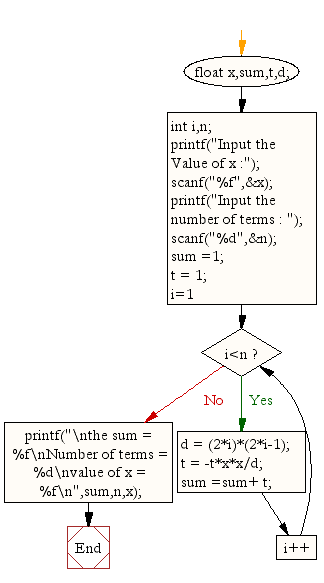



C Exercises Calculate The Sum Of The Series 1 X 2 2 X 4 4 W3resource




Harmonic Series Mathematics Wikiwand
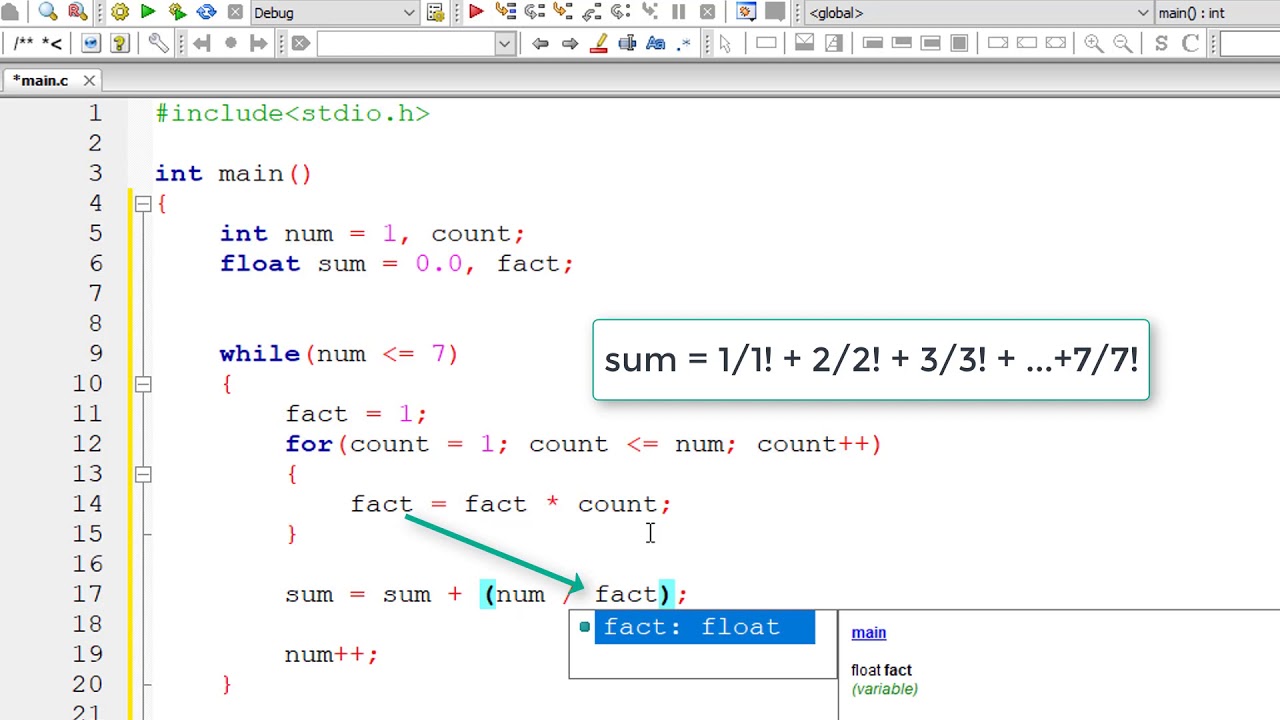



C Program To Find Sum Of Series 1 1 2 2 3 3 N N Youtube




Infinite Series




Why Does The Series Sum N 1 Infty Frac1n Not Converge Mathematics Stack Exchange




Ex 9 4 4 Find Sum Of Series 1 1 X 2 1 2 X 3 1 3 X 4




Find The Sum Of The Series Sum N 1 Infty Frac 3n 2 N Mathematics Stack Exchange




Find A Formula For The General Term A N Not The Chegg Com



Faculty Math Illinois Edu Jpascale Courses 11 M408d Notes Hw4 Sol Pdf



Key Concepts In Computer Science Assignment 10 All Test Answers




1 2 1 4 1 8 1 16 Wikipedia




How To Find 1 2 1 4 1 8 Video Lesson Transcript Study Com




How To Prove A Formula For The Sum Of Powers Of 2 By Induction Mathematics Stack Exchange
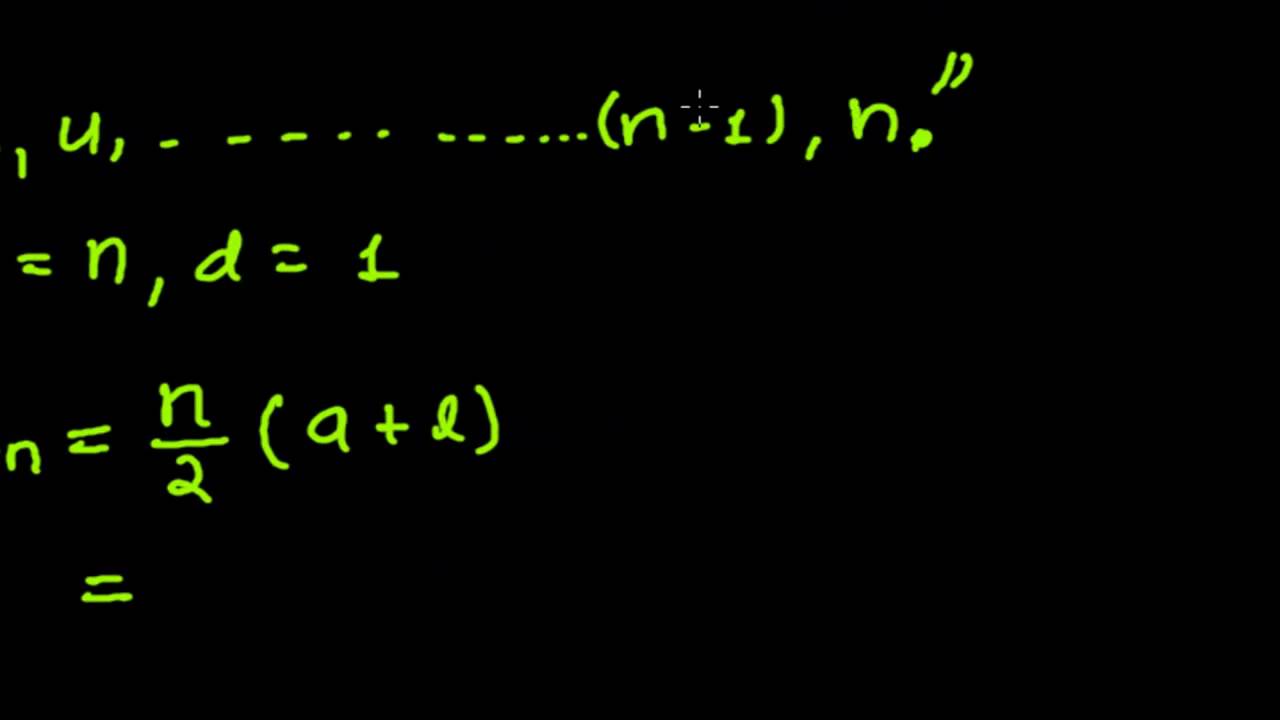



How To Sum The Integers From 1 To N 8 Steps With Pictures



What Is The Sum Of 1 2 1 4 1 8 Quora




Python Program To Calculate Sum Of Series 1 2 3 N



What Is The Sum Of The Series Math 1 1 2 1 3 1 4 1 5 Math Up To Infinity How Can It Be Calculated Quora




Understand The Formula For Infinite Geometric Series Video Lesson Transcript Study Com




1234n Formula




1 Determine Whether The Series Converge Or Diverge Chegg Com




Geometric Series Wikipedia




Find The Sum Of The Series 2 2 4 2 6 2 2 N 2




Why 1 2 3 4 To Infinity 1 12 In 3 Minutes Youtube




Example 12 Find Sum Of First N Terms And Of First 5 Terms




1 2 1 4 1 8 1 16 Wikipedia




n2 Formula




Ex 9 4 4 Find Sum Of Series 1 1 X 2 1 2 X 3 1 3 X 4




A Using Formula 2 Find The Sum Of The Series Chegg Com



1



Find The Sum Of The Series 1 11 111 1111 Upto N Terms Geeksforgeeks




How To Find The Sum Of The Series Math Frac 1 1 Cdot 2 Frac 1 2 Cdot 3 Frac 1 3 Cdot 4 Frac 1 4 Cdot 5 Ldots Frac 1 N N 1 Quora




How To Proceed Further In This Arithmetico Geometric Progression Problem Mathematics Stack Exchange




How To Sum The Integers From 1 To N 8 Steps With Pictures
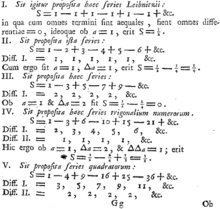



1 2 3 4 Wikipedia




Convergent Divergent Geometric Series With Manipulation Video Khan Academy




Divide The Sum Of 2 1 4 And 5 1 5 And Product Of 2 1 2 And 2 3 Brainly In



1




Ali Added The Following Series If Fraction How Many More Fraction In This Series He Must Add To Get The Answer Equal To Onevor More Than One 1 2 1 4 1 Mathematics Topperlearning Com 8ycaaeuu




Find The Sum Of N Terms Of The Series 1 2 4 1 4 6



1




What Is The Sum Of 1 1 3 2 1 3 3 1 3 N Quora



1



Is There A Name For This Mathematical Sequence Math 1 2 4 7 11 16 22 29 37 46 56 Math Quora




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange




Proof 1 1 1 4 1 9 1 16 1 25 Pi 2 6 Youtube




Sum Of N Squares Part 1 Video Khan Academy
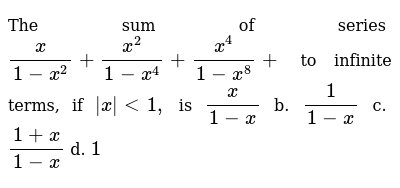



The Sum Of Series X 1 X 2 X 2 1 X 4 X 4 1 X 8 To Infi




How To Sum The Integers From 1 To N 8 Steps With Pictures



Python Challenges 1 Exercises Practice Solution W3resource




Strong Integral Test On Sequences And Harmonic Sums Chegg Com
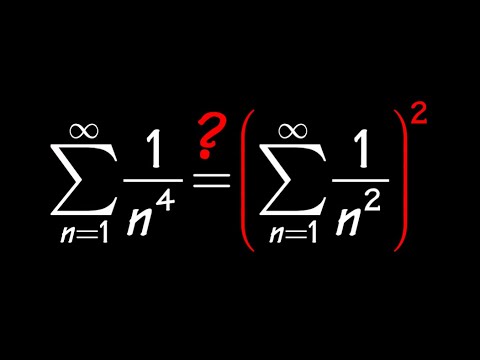



Sum Of 1 N 4 Fourier Series Parseval S Theorem Youtube




Ex 4 1 9 Prove 1 2 1 4 1 8 1 2n 1 1 2n




Math 1210 Solutions To Assignment 1 Fall 12 1 A Use



C Program To Find The Sum Of Series 1 4 2 4 3 4 N 4 Stack Overflow




How To Sum The Integers From 1 To N 8 Steps With Pictures



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




Paradox 1 1 2 1 3 1 4 0 The Simpsons And Their Mathematical Secrets
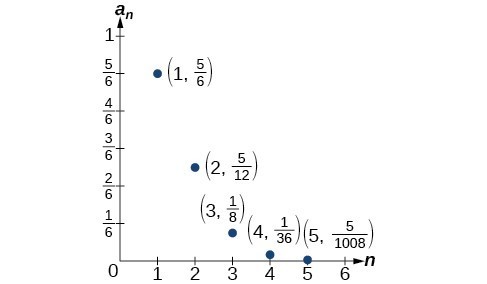



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra



How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora




Find The Sum Of N Terms Of The Series 1 2 4 1 4 6




Show That The Sum Of The Cubes Of The First N Natural Numbers Equal




Defining And Using Sequences And Series Ppt Download




The Viral 1 4 5 Puzzle The Correct Answer Explained Mind Your Decisions




Basel Problem Wikipedia




The A M Of The Series 1 2 4 8 16 2 N Is Youtube




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter Geometric Progressions Download Free Pdf Available




Find The Sum To N Terms 1 2 2 2 2 3 3 2 4 Youtube




Using Formula 2 Find The Sum Of The Series Sigma N Chegg Com




Geometric Series Wikipedia




Partial Sums Formula For Nth Term From Partial Sum Video Khan Academy
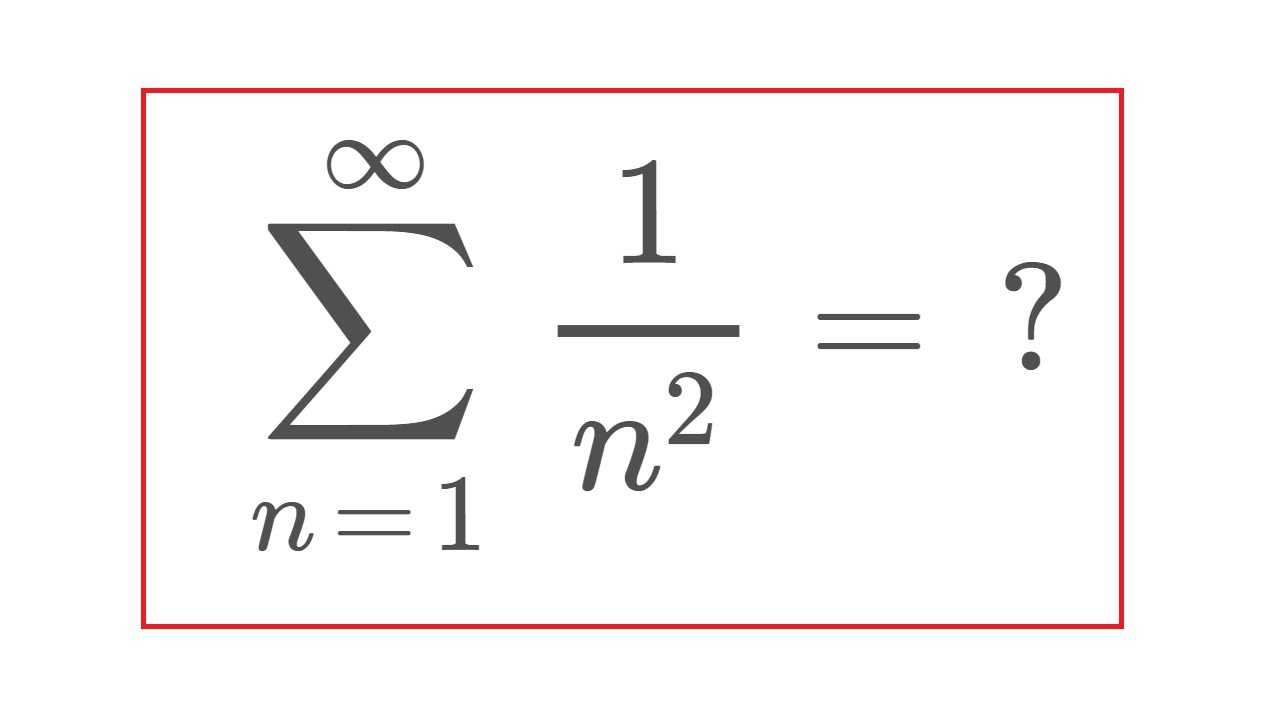



Sum Of 1 N 2 Youtube




Summation Notation Rules Examples Video Lesson Transcript Study Com




Example 1 Find Partial Sums Solution S 1 1 2 0 5 S 2 S 3 Find And Graph The Partial Sums S N For N 1 Ppt Download




Intro To Series What Is 1 2 1 4 1 8 1 16 Youtube
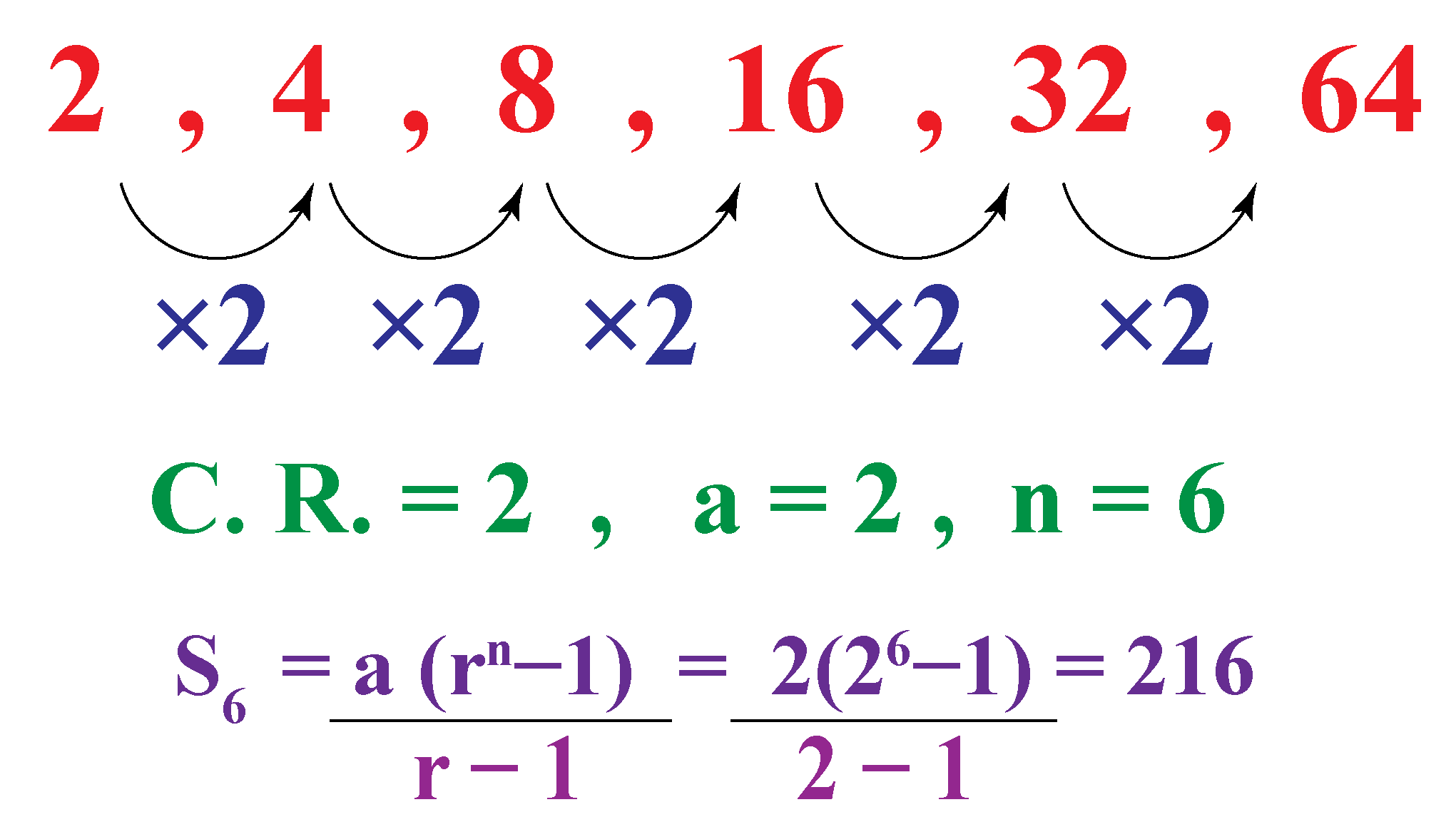



Sum Of A Gp Geometric Progression Solved Examples Cuemath




Find Sum Of The Following Ap 1 1 N 1 2 N 1 3 N Upto Nth Terms Brainly In




Consider The Conditionally Convergent Series Chegg Com


